Lcm Of 15 And 6
plugunplug
Sep 22, 2025 · 6 min read
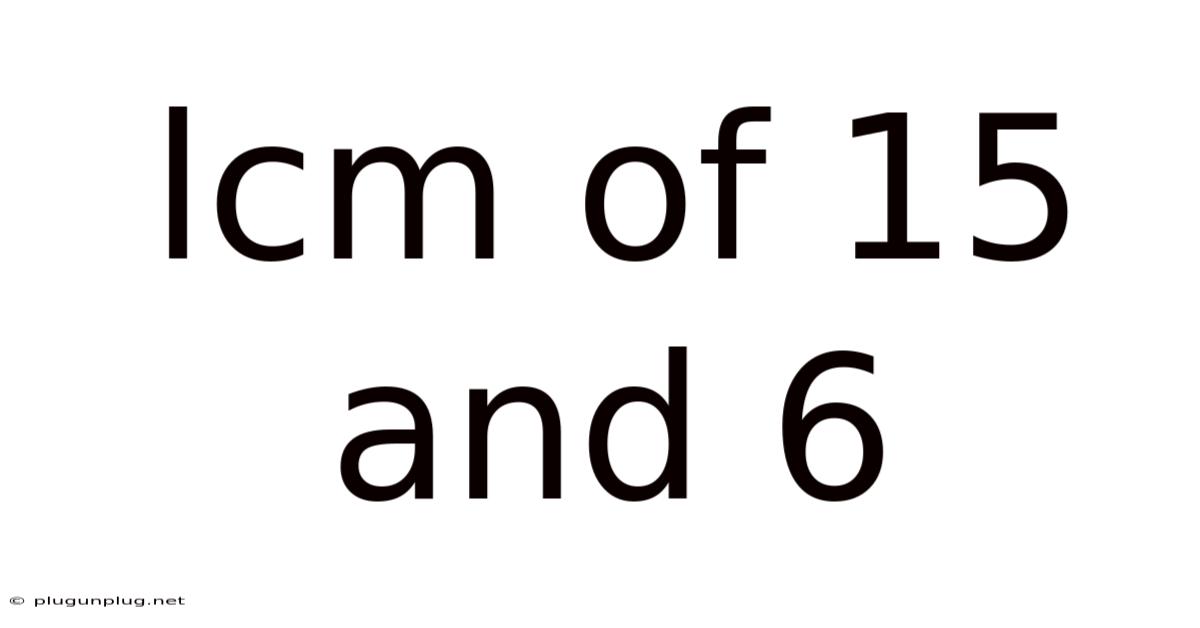
Table of Contents
Finding the LCM of 15 and 6: A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) of two numbers, like 15 and 6, might seem like a simple arithmetic task. However, understanding the underlying concepts and different methods for calculating the LCM provides a valuable foundation for more advanced mathematical concepts. This article will explore various approaches to finding the LCM of 15 and 6, explaining the principles behind each method and highlighting their applications in broader mathematical contexts. We'll delve into prime factorization, listing multiples, and using the greatest common divisor (GCD), ensuring a comprehensive understanding suitable for students and anyone interested in refreshing their mathematical skills.
Understanding Least Common Multiples (LCM)
Before we dive into calculating the LCM of 15 and 6, let's solidify our understanding of what an LCM actually represents. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the numbers you're considering as factors. In simpler terms, it's the smallest number that all the numbers can divide into evenly.
For example, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, 30, and so on. The least common multiple, therefore, is 6.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers like 15 and 6. We simply list the multiples of each number until we find the smallest common multiple.
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105...
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 54, 60...
By comparing the lists, we see that the smallest number appearing in both lists is 30. Therefore, the LCM of 15 and 6 is 30.
This method is simple and intuitive, but it becomes less efficient as the numbers get larger. Imagine trying to find the LCM of 1575 and 2310 using this method – it would be incredibly time-consuming.
Method 2: Prime Factorization
Prime factorization is a more powerful and efficient method, particularly for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime factorize 15: 15 = 3 x 5
- Prime factorize 6: 6 = 2 x 3
Now, we take the highest power of each prime factor present in either factorization:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2
- The highest power of 3 is 3¹ = 3
- The highest power of 5 is 5¹ = 5
To find the LCM, we multiply these highest powers together: 2 x 3 x 5 = 30.
Therefore, the LCM of 15 and 6 is 30. This method is far more efficient than listing multiples, especially for larger numbers. It provides a structured approach that guarantees finding the LCM without exhaustive listing.
Method 3: Using the Greatest Common Divisor (GCD)
The greatest common divisor (GCD) is the largest number that divides both numbers without leaving a remainder. There's a useful relationship between the LCM and the GCD:
LCM(a, b) x GCD(a, b) = a x b
where 'a' and 'b' are the two numbers.
-
Find the GCD of 15 and 6: We can use the Euclidean algorithm to find the GCD.
- 15 = 2 x 6 + 3
- 6 = 2 x 3 + 0 The last non-zero remainder is the GCD, which is 3.
-
Apply the LCM-GCD relationship: LCM(15, 6) x GCD(15, 6) = 15 x 6 LCM(15, 6) x 3 = 90 LCM(15, 6) = 90 / 3 = 30
Therefore, the LCM of 15 and 6 is 30. This method leverages the relationship between LCM and GCD, providing an alternative approach to calculating the LCM. The Euclidean algorithm for finding the GCD is particularly efficient for larger numbers.
Illustrative Examples: Applying LCM in Real-World Scenarios
Understanding LCM extends beyond abstract mathematical exercises. It finds practical applications in various real-world scenarios:
-
Scheduling: Imagine two buses depart from a station at different intervals. One departs every 15 minutes, and the other every 6 minutes. The LCM (30 minutes) determines when both buses will depart simultaneously again. This principle applies to various scheduling problems, such as coordinating events or tasks with different repeating cycles.
-
Fractions: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators. For example, to add 1/6 and 1/15, we need to find the LCM of 6 and 15, which is 30. This allows us to rewrite the fractions with a common denominator before performing the addition.
-
Tiling and Patterns: LCM plays a role in designing repeating patterns or tiling arrangements. If you have tiles of two different sizes, the LCM of their dimensions will determine the smallest repeating unit for a seamless pattern.
-
Gear Ratios: In mechanics, gear ratios rely on the LCM to determine when gears will align again after a certain number of rotations. This is crucial in designing synchronized mechanical systems.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The Least Common Multiple (LCM) is the smallest number that is a multiple of both numbers. The Greatest Common Divisor (GCD) is the largest number that divides both numbers without leaving a remainder. They are inversely related; a larger GCD implies a smaller LCM, and vice versa.
Q2: Can the LCM of two numbers be one of the numbers?
A2: Yes, if one number is a multiple of the other. For example, the LCM of 6 and 12 is 12.
Q3: Is there a formula for LCM?
A3: Yes, besides the relationship with GCD (LCM(a, b) = (a x b) / GCD(a, b)), there's also a formula based on prime factorization. If the prime factorization of a is p1^a1 * p2^a2 * ... and the prime factorization of b is p1^b1 * p2^b2 * ..., then the LCM(a, b) = p1^max(a1, b1) * p2^max(a2, b2) * ...
Q4: How do I find the LCM of more than two numbers?
A4: You can extend the prime factorization method or the GCD-based method to include more than two numbers. For prime factorization, you consider the highest power of each prime factor present in any of the numbers. For the GCD method, you would need to find the GCD of all numbers pairwise and then use the relationship iteratively.
Conclusion
Finding the LCM of 15 and 6, while seemingly simple, provides a gateway to understanding fundamental mathematical concepts. This article has explored three distinct methods – listing multiples, prime factorization, and the GCD approach – each offering different levels of efficiency and applicability depending on the numbers involved. Understanding the underlying principles and choosing the appropriate method is crucial for tackling more complex problems involving LCMs. Moreover, appreciating the real-world applications of LCM highlights its relevance beyond theoretical mathematics, showcasing its practical use in diverse fields ranging from scheduling and fractions to tiling and mechanical systems. Mastering LCM calculation is not just about arithmetic proficiency; it's about developing a deeper understanding of number theory and its impact on various aspects of our lives.
Latest Posts
Latest Posts
-
Double Angle Formula Cos 2x
Sep 22, 2025
-
Temp For Water To Freeze
Sep 22, 2025
-
Average 11 Year Old Height
Sep 22, 2025
-
5 7 Inch In Cm
Sep 22, 2025
-
How To Solve Quadratic Equation
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 15 And 6 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.