What Is 10 Of 30000
plugunplug
Sep 17, 2025 · 5 min read
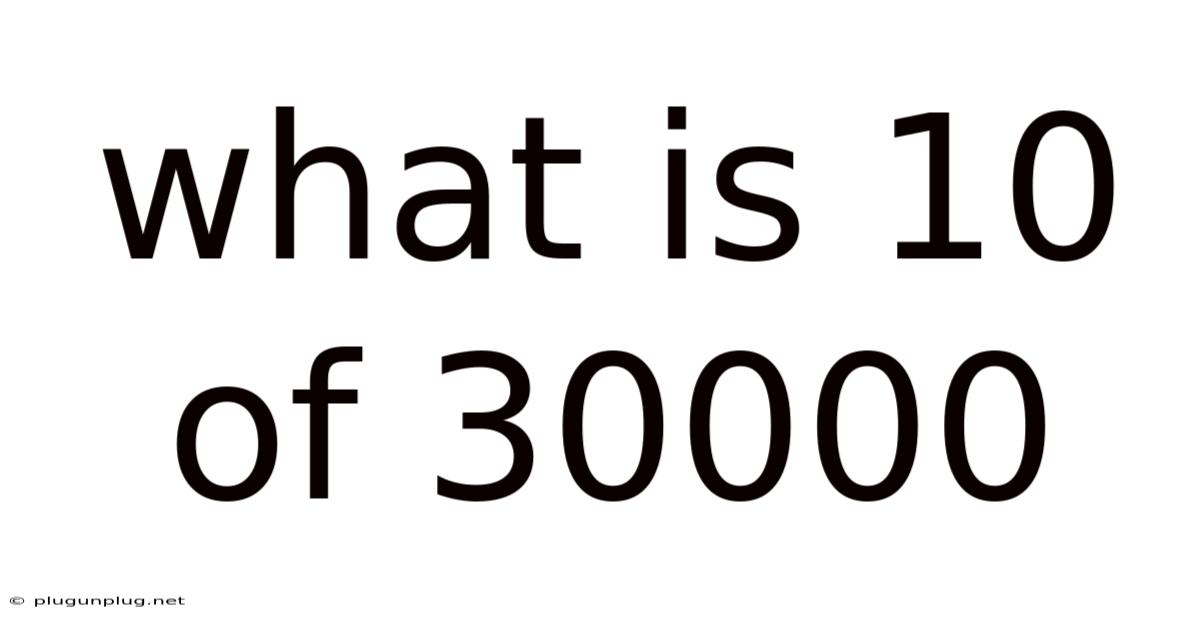
Table of Contents
What is 10/30000? Understanding Fractions and Percentages in Context
This article explores the simple mathematical problem of "What is 10/30000?" But instead of simply providing the answer, we'll delve into the broader concepts of fractions, percentages, and how to understand and apply these concepts in various real-world scenarios. This will help you not only solve this specific problem but also equip you with the skills to tackle similar calculations with confidence. We'll cover different methods of solving the problem, discuss its practical applications, and address some common questions surrounding fractions and percentages.
Understanding Fractions
A fraction represents a part of a whole. It consists of two numbers: a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts the whole is divided into. In our case, 10/30000, 10 is the numerator and 30000 is the denominator. This fraction signifies that we have 10 parts out of a total of 30000 equal parts.
Calculating 10/30000
There are several ways to calculate 10/30000:
1. Direct Division: The simplest method is to divide the numerator (10) by the denominator (30000). Using a calculator or performing long division, we get:
10 ÷ 30000 = 0.0003333...
This decimal representation shows that 10 out of 30000 represents a very small portion of the whole.
2. Simplification: Before division, we can simplify the fraction by finding the greatest common divisor (GCD) of the numerator and denominator. In this case, the GCD of 10 and 30000 is 10. Dividing both the numerator and denominator by 10, we get:
10 ÷ 10 / 30000 ÷ 10 = 1/3000
This simplified fraction is easier to work with, although the decimal representation remains the same after division:
1 ÷ 3000 = 0.0003333...
3. Percentage Conversion: To express the fraction as a percentage, we multiply the decimal result by 100:
0.0003333... × 100 ≈ 0.0333%
This means that 10 out of 30000 represents approximately 0.0333% of the whole.
Practical Applications and Real-World Examples
Understanding fractions and percentages is crucial in numerous real-world scenarios. Here are some examples illustrating the practical application of calculating 10/30000:
-
Sampling and Surveys: Imagine a survey conducted with 30,000 participants. If 10 respondents answered a specific question in a particular way, the fraction 10/30000 represents the proportion of respondents with that specific answer. This data can be used to understand the overall sentiment or opinion within the larger population.
-
Manufacturing Defects: A factory produces 30,000 units of a product. If 10 units are found to be defective, 10/30000 represents the defect rate. This information is critical for quality control and improving the manufacturing process.
-
Financial Analysis: In financial modeling, fractions and percentages are extensively used. For instance, if a company has total assets worth 30,000 units and a specific liability amounts to 10 units, the fraction 10/30000 represents the proportion of this liability to the total assets.
-
Scientific Experiments and Data Analysis: In scientific research, fractions and percentages are fundamental tools for data analysis. Experimental results are often presented as fractions or percentages to illustrate proportions and relationships between variables. A fraction like 10/30000 could represent a small but potentially significant finding within a large data set.
-
Probability: Imagine you have 30,000 lottery tickets, and 10 of them are winning tickets. The probability of winning with a single ticket is 10/30000.
Understanding the Significance of Small Percentages
The result of 10/30000, approximately 0.0333%, might seem insignificant at first glance. However, depending on the context, this small percentage could have significant implications. For instance, in a large-scale manufacturing process, a seemingly small defect rate of 0.0333% could still translate to a substantial number of defective products. Similarly, in a large-scale survey, a small percentage could represent a significant trend or opinion shift within a population.
Frequently Asked Questions (FAQ)
Q1: How can I convert a fraction to a decimal?
A1: To convert a fraction to a decimal, divide the numerator by the denominator. For example, 10/30000 = 0.0003333...
Q2: How can I convert a decimal to a percentage?
A2: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol. For example, 0.0003333... × 100 = 0.0333%
Q3: What is the significance of simplifying fractions?
A3: Simplifying fractions makes them easier to understand and work with. It also allows for easier comparisons between different fractions.
Q4: Can I use a calculator for this type of calculation?
A4: Yes, calculators are a convenient tool for solving these problems, especially for larger numbers.
Q5: Are there any online tools or software that can help with fraction and percentage calculations?
A5: Yes, many online calculators and software programs are available for performing fraction and percentage calculations. These can be particularly helpful for more complex calculations.
Conclusion: Beyond the Numbers
This article aimed to go beyond simply providing the answer to "What is 10/30000?" We've explored the fundamental concepts of fractions and percentages, shown different methods of calculation, highlighted real-world applications, and addressed common questions. The ultimate goal is not just to solve a mathematical problem but to understand the underlying principles and their significance in various contexts. Remember that even seemingly small fractions and percentages can hold significant meaning, depending on the scenario in which they are used. Mastering these concepts empowers you to analyze data, make informed decisions, and navigate the quantitative aspects of the world around you with greater confidence. By understanding these basic principles, you develop a crucial skill applicable across a vast spectrum of disciplines and daily life.
Latest Posts
Latest Posts
-
Formula For Combustion Of Propane
Sep 17, 2025
-
How Much Is 3 4
Sep 17, 2025
-
How Much Are Marlboro Cigarettes
Sep 17, 2025
-
What Does Mmorpg Stand For
Sep 17, 2025
-
Three Types Of Nuclear Radiation
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 30000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.